Let's tackle chapter 1.3 of the ShaderX³ book and more particularly the part called Twist. The twist effect is cool but the implémentation has been done with Direct3D shaders and above all, the image at the beginning of the chapter showing a nice twisted cube has no implementation.

The effect I wish is the following:

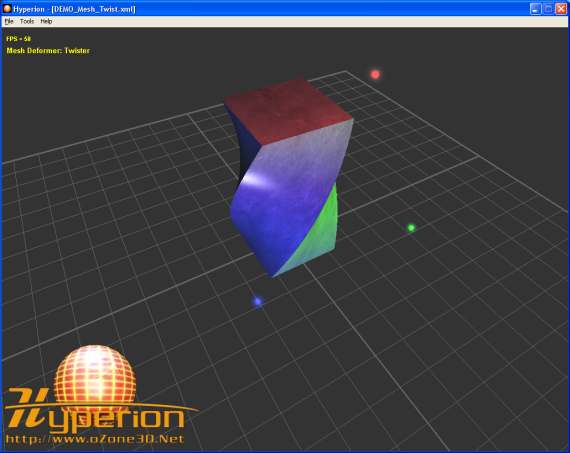
The twist effect consists in deforming the mesh's vertices along a certain axis. In the demo, the deformation axis is the Y one.

In comparison to the surface deformer, the mathematics is less complex and remains limited to few sin/cos cleverly organized functions. The mathematical relation to twist the mesh around the Y axis is the following:

From this relation and using an angle value based on both time and vertex's position we can achieve the effect shown in the previous image. The objective is to move the vertices with an angle that is proportinal to the elapsed time and the vertex's height. The vertices that have a height equal to 0 will not move while those localized in the upper part of the cube will be deformed with a maximal angle.

The following code is that of the vertex shader. The vertex shader's core is the DoTwist() function that is used to tranform a vertex.

uniform float time;
uniform float height;
uniform float angle_deg_max;
varying vec3 normal, lightDir[3], eyeVec;


vec4 DoTwist( vec4 pos, float t )
{
	float st = sin(t);
	float ct = cos(t);
	vec4 new_pos;
	
	new_pos.x = pos.x*ct - pos.z*st;
	new_pos.z = pos.x*st + pos.z*ct;
	
	new_pos.y = pos.y;
	new_pos.w = pos.w;

	return( new_pos );
}


void main(void)
{
	float angle_deg = angle_deg_max*sin(time);
	float angle_rad = angle_deg * 3.14159 / 180.0;
	
	float ang = (height*0.5 + gl_Vertex.y)/height * angle_rad;
	
	vec4 twistedPosition = DoTwist(gl_Vertex, ang);
	vec4 twistedNormal = DoTwist(vec4(gl_Normal, ang), 

	gl_Position = gl_ModelViewProjectionMatrix * twistedPosition;
	
	vec3 vVertex = vec3(gl_ModelViewMatrix * twistedPosition);
	lightDir[0] = vec3(gl_LightSource[0].position.xyz - vVertex);
	lightDir[1] = vec3(gl_LightSource[1].position.xyz - vVertex);
	lightDir[2] = vec3(gl_LightSource[2].position.xyz - vVertex);
	eyeVec = -vVertex;

	normal = gl_NormalMatrix * twistedNormal.xyz;
	
	gl_TexCoord[0] = gl_MultiTexCoord0;
}

We are in a situation where the vertex normal vector calculation is simple. Indeed, the same function is used to change the vertex's position and to compute its normal.