La formule d’Euler pour les graphes connectés vous connaissez? Je l’ai decouverte il n’y a pas longtemps en tombant sur ce cours de math pour gamins de 8 ans.
Cette formule découverte par le suisse Euler est toute simple:
V – E + R = 2
Cette égalité, valable pour les graphes connectés planaires, nous dit que le nombre de sommets (V pour vertices) moins le nombre de cotés (E pour edges) additionné du nombre de faces (ou regions R) est toujours egal à 2.
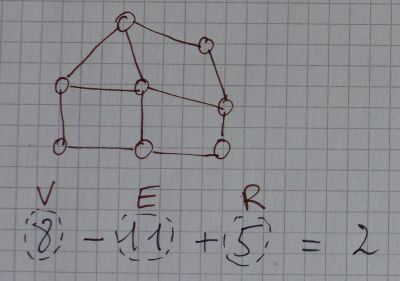
Tant que les segments qui représentent les cotés ne se croisent pas (pas d’intersection), cette formule est vraie pour n’importe quel graphe:
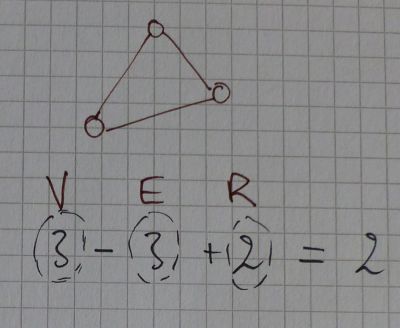
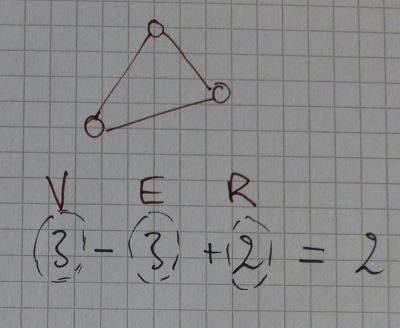
Le triangle précédant possède 3 Vertices, 3 Edges et défini 2 Regions (ou espaces: à l’intérieur du triangle et à l’exterieur du triangle).
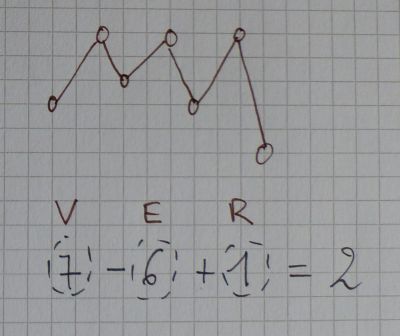
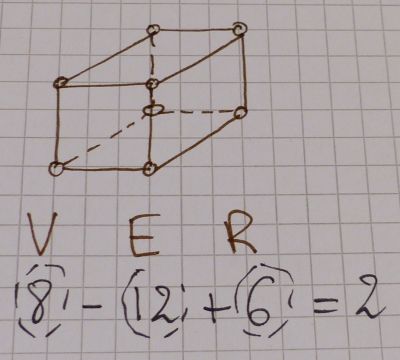
Et la formulke d’Euler est aussi applicable aux objets 3D. Dans le cas des solides 3D, les régions sont les faces. Le cube par example, a 8 Vertices, 12 Edges et 6 Regions: